Research Project A02

Exchange processes across a porous-medium free-flow interface occur in a wide range of environmental, technical and bio-mechanical systems. The primary objectives of this project are to (i) analyse and improve the theory, as well as (ii) offer solution methods for non-isothermal, multi-phase, multi-component flow and transport processes at a porous-medium free-flow interface and (iii) investigate the influence of these processes on both the porous medium and free-flow region for various application scales.

The challenge of including scale-dependent, interface-driven processes into mathematical and numerical models for systems of coupled free flow and porous-medium flow is the primary object of research of project A02. We found that existing models usually operate on either the pore scale or on the REV scale which has the following drawbacks: pore-scale models provide a detailed physical insight into various types of processes but their prohibitively high computational demand makes them only applicable to relatively small domains. On the other hand, the higher degree of computational efficiency provided by REV-scale models comes at the price of losing potentially process-relevant sub-scale information. In addition, several assumptions and simplifications commonly involved in REV-scale modelling can only be justified for a limited range of applications and flow conditions.

Our main goal is the development of new model concepts combining the strengths of both pore-scale and REV-scale approaches.

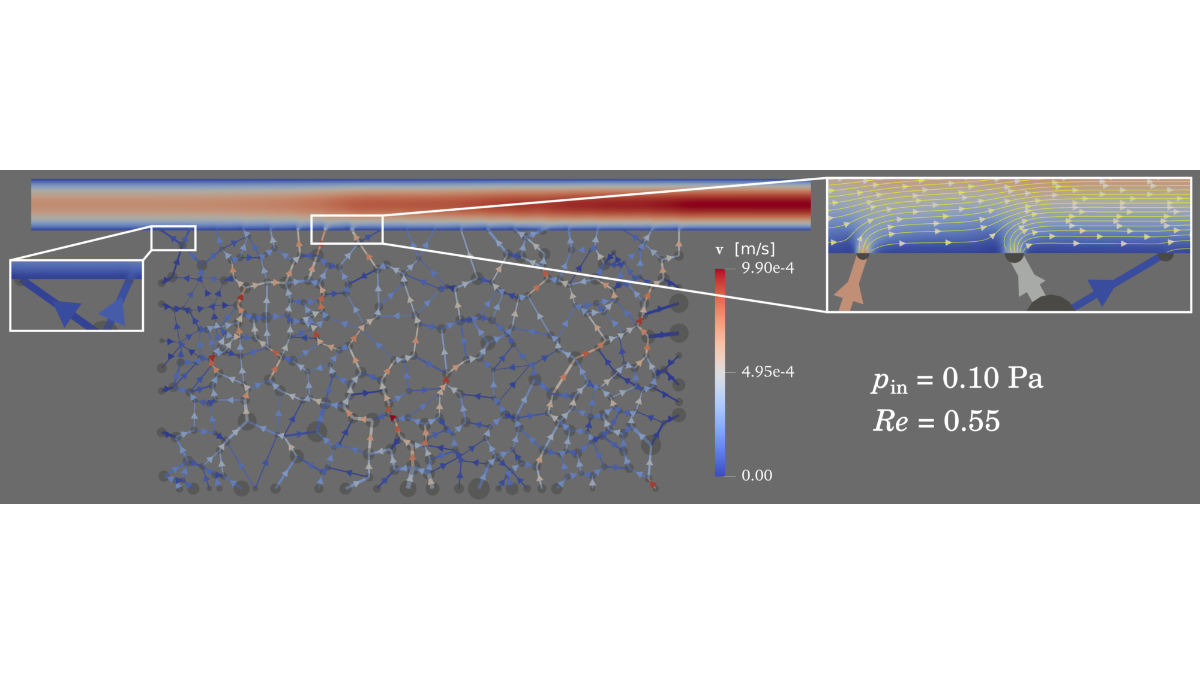
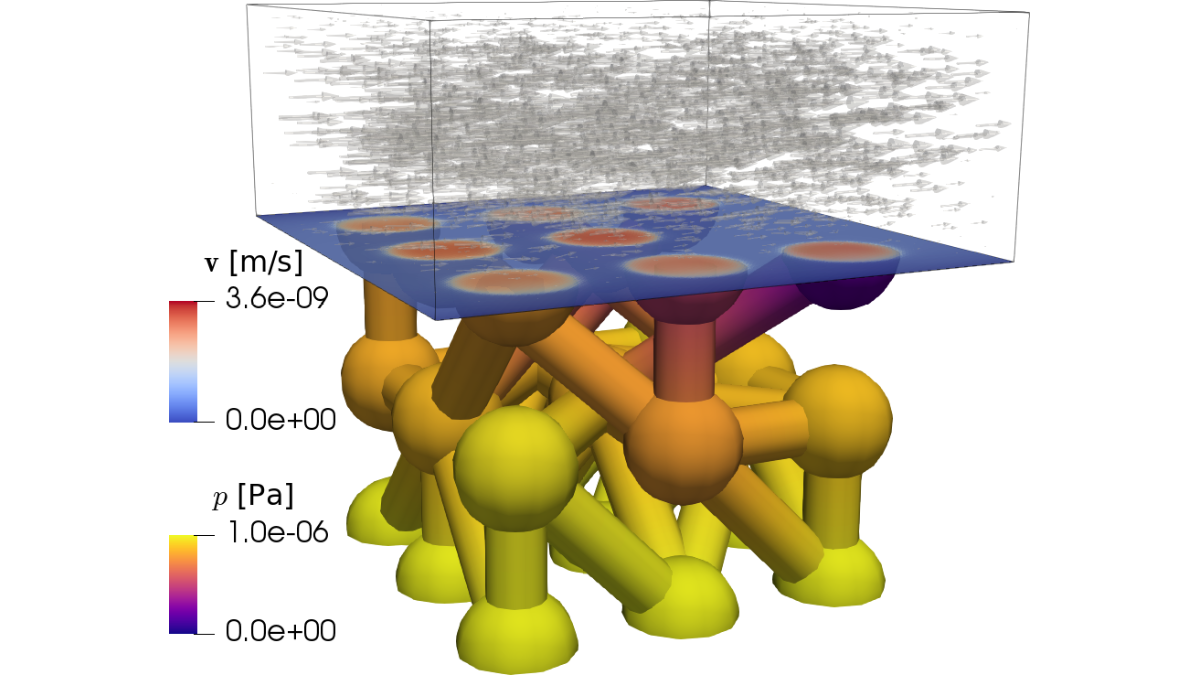
During the first funding period (FP1), we laid the foundations for the development of these cross-scale concepts. A new hybrid modelling approach was developed to account for pore-scale processes in the interface-region. These are considered by a pore-network model (PNM) that couples the REV domain with the free-flow domain.

We developed interface conditions for the coupling between the free-flow domain and the pore-network model, ensuring the conservation mass and momentum across the discrete pore-scale coupling interface. Following this, conditions for coupling the pore-network model with the REV-scale bulk porous medium were developed, resulting in a three-domain model concept where the pore-network models serves as an interface region between the free-flow domain and the bulk porous part. The coupled free-flow/pore network model was extended for non-isothermal, multi-component two-phase flow in the network part, allowing the simulation of an evaporation process in ample detail.

To obtain the unknown coupling paramters comprised in the coupling condtions the interface exchange processes have been investigated with pore-resolved direct numerical simulations (DNS) resolving all relevant time and length scales in the pore-space complemented by  pore-scale experimental data provided by our collaboration partners at Utrecht University. 

In the second funding period (FP2), the influence of surface roughness at the pore-scale and surface topology at the macro-scale of permeable surfaces including multiphase systems was analysed. This allowed detailed physical insights into the interaction between the porous medium and the external free-flow and enabled the improvement of the efficient hybrid modeling approach that can now be used for the efficient modeling of such systems. This was achieved by introducing coupling conditions for arbitrary flow conditions developed in A03.

To further improve the PNM as the key part in the hybrid modeling approach a novel, fully implicit PNM with increased robustness, efficiency and accuracy for non-isothermal multi-component multiphase systems was developed. Building on this, a dual pore-network model (DPNM) was developed to capture the conjugate heat transfer between solid and fluid phases.

With respect to the pore-local closure relations used by the PNM which are used to bride the scale gap from fully resolved pore space to single discretization points per pore, pore resolved simulations have been condcted. This enabled us to create a dataset for new pore-local capillary pressure-saturation relations, dependend on intrinsic wettability, viscosity ratio and capillary number. The quantitative data was compared to experimental data form our eternal partners at Utrecht University and showed the limitations of classical pore-local relations used in pore-network models (PNMs).

To improve the REV-scale modelling also comprised in the hybrid modeling approach an upscaling from the pore-scale to the REV-scale was developped.

The overall aim of FP3 is to accurately describe the evaporation process in the interfacial region on the one hand and possible precipitation processes of salt on the other. Therefore, the existing evaporation model in our DNS framework will be extended to accurately capture the evaporation processes in the vicinity of three-phase contact lines. This will allow us to continue our strategy of performing pore-resolved simulations that resolve all relevant time and length scales and use them to develop the necessary coupling conditions for the cross-scale hybrid modelling concept and to provide the required effective parameters for the REV-scale models. Here we will collaborate with research project A03 to develop new coupling conditions that account for changes in liquid distribution during evaporation. To quantify their dependencies on sub-scale characteristics, such as pore geometry and liquid distribution, we continue our work with D03-Flemisch/Oladyshkin and develop a corresponding surrogate model. The verification of the selected coupling approaches for the evaporation process will be compared with the pore-resolved simulations and with experiments.

The developed dynamic PNM enables an implicit solution of two-phase flow, accounting for pore space evolution and pore constriction due to salt precipitation. This advancement enhances our ability to predict drying and salt deposition patterns, supporting the goals of the vision project.

Validation of drying and salt precipitation patterns with experimental data

The drying and salt precipitation patterns obtained from a quasi-static pore-network model (PNM) are first compared with those from a dynamic PNM. To ensure accuracy, we validate than our models against microfluidic experiments conducted by PML (Z02-Karadimitriou/Steeb) in collaboration with Bo Guo’s team at the University of Arizona.