Research Project C02

Combined multi-phase flow and reactive transport processes in porous media are encountered for many important fields in environmental and biological sciences as well as in technological applications. These processes occur and interact at different spatial scales. In this project, we consider for an REV scale of cm-length different immiscible fluid and solid phases which are separated by interfaces. These move in the pore space due to flow and bio-chemical processes like the precipitation and dissolution of crystals, or the growth and degradation of biofilms.

The main challenge is to understand the evolution of the interfaces, the impact on the pore geometry, and further on the REV-scale behaviour of the system. This renders traditional approaches focusing on processes at one scale to be inadequate: at the smallest scales these are too complex and hence computationally prohibitive, whereas at the larger scales they disregard essential information provided by the smaller scales.

The goal of this project is to construct reliable and computable mathematical models for multi-scale problems in complex domains, which account for the interfaces evolving at the pore scale. Such issues will be addressed within a generic mathematical and computational framework, which covers in particular multi-phase flow and bio-chemical processes. The outcome will be a family of new pore-scale models, rationally derived effective (REV-scale) mathematical models and appropriate numerical algorithms.

We have developed multiple-diffuse interface models for fluid-solid interfaces. The first model describes the flow of one fluid phase and uses an Allen-Cahn evolution for the phase field variable. The second model describes the incompressible flow of two immiscible fluids and uses a ternary Cahn-Hilliard evolution for the phase-field variables. Both models modify the Navier-Stokes equations for incompressible fluid flow to hold only in the fluid volume fraction The solid phase is a mineral that can grow or shrink due to precipitation or dissolution, depending on the concentration of different solutes in the fluid phases. These concentrations are not known a-priori but represent model unknowns. The Cahn-Hilliard model has been shown to obey the second law of thermodynamics for a novel free-energy formulation.

For both models a sharp-interface formulation is recovered for vanishing interfacial width by using matched-asymptotic analysis. Notably, the Cahn-Hilliard model is able to realise Navier-slip conditions for solid-fluid interfaces in the limit.

Building on the pore-scale phase-field models, different REV-scale models have been derived. For the one-phase Allen-Cahn model this is achieved by assuming periodicity w.r.t. the fast variables at the micro-scale, and by employing homogenisation techniques. The result is a Darcy-type law at the REV scale, in which the porosity, the permeability and the effective diffusion still depend on the micro-scale characteristics (and in particular the amount of the mineral and its shape) encountered at each macro-scale point. These characteristics are described through cell problems in terms of the phase-field variable.

Further, for this REV-scale model, we have developed a multi-scale iterative scheme. In this scheme, the pore- and the REV-scale model components are coupled iteratively, which reduces significantly the complexity of the algorithm when compared to a monolithic approach. Next, linear iterative schemes building on the L-scheme are used to solve the non-linear cell problems at the pore scale. The macro-scale quantities like porosity, absolute permeability and the diffusion tensor are computed adaptively, based on an active-passive node strategy.

To derive a REV-scale model for the two-phase Cahn-Hilliard model, we considered it in the simplified geometry of a thin strip. The homogenised model, which is derived by transversal averaging, consists of up-scaled equations for ion transport and total flux, while the strongly non-linear phase-field equations do not up-scale. By using explicit upwinding for the transport terms in the numerical implementation, the cell problems still decouple and can be evaluated in parallel. We also find asymptotic consistency, that is, the sharp-interface limit of the up-scaled model is the same as the one obtained from up-scaling the sharp-interface limit.

For the Navier-Stokes Cahn-Hilliard model, we developed a finite-element method, with Taylor–Hood elements for the flow variables velocity and pressure, and second-order Lagrange elements for the ion concentration and the phase-field parameters. The implementation was done in DUNE-PDELab using ALU-Grid routines, thus being fully compatible with Dumux. Notably, this software framework allows for adaptive grid generation.

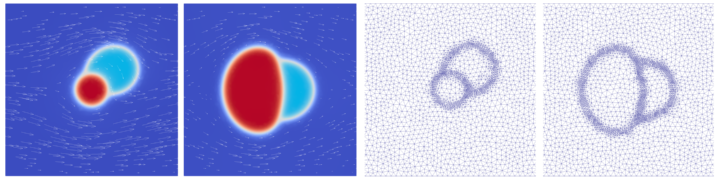
With this code, we ran a study in order to compare simulation results with experimental findings on enzymatically-induced calcite precipitation (EICP). This study investigates the growth of calcium-carbonate crystals in a micro-fluidic EICP experiment that consists of a setup of four pore bodies connected by pore throats. The model’s capability to reproduce the direction and volume of crystal growth has been analysed. The mechanisms that dominate crystal growth are complex. They depend on the local flow field as well as on concentrations of solutes. In particular, we succeeded to explain why crystal aggregates prefer to grow in up-stream flow direction and towards the center of the flow channels, where the volume growth rate is also higher due to better supply.

We plan advance the pore-scale modelling to include more detailed interfacial physics, to cover asymptotic flow regimes and to account for sub-structured pore geometries. Based upon these developments we aim at the derivation of new REV-scale models. This includes not only effective models for simplified pore geometries but also two-scale approaches allowing complex pore-scale dynamics. A specific challenge will be the realisation of up-scaled multiple-porosity models or multi-scale models for porous media flow involving sub-pore scales.

Finally, the model-oriented research will go along with the development of efficient numerical tools for both, the pore-scale models as well as the multi-scale approaches. The latter require in particular model-adaptive techniques for the effective selection of cell problems.

We work in close cooperation with the Computational Mathematics group (CMAT) at Hasselt University. The upscaling of phase field models was done in collaboration with Hasselt University, sharing knowledge of homogenisation techniques for different regimes and geometric assumptions. In particular for the upscaling in a thin strip our cooperation includes surface tension effects between two fluid phases. The development of a multi-scale iterative scheme for the upscaled Allen-Cahn model is also a collaboration with Hasselt University.

We cooperate on the topic of upscaled models for incompressible two-phase flow, including hysteresis.