New joint publication by the University of Stuttgart and the University of Bergen (Norway), published in Numerical Methods for Partial Differential Equations. The work has been developed within SFB 1313 research project B03.
Towards hybrid two-phase modelling using linear domain decomposition
Authors
- David Seus (University of Stuttgart)
- Florin A. Radu (University of Bergen, SFB 1313 Mercator Fellow, research project B03)
- Christian Rohde (University of Stuttgart, SFB 1313 research projects B03 and C02)
Abstract
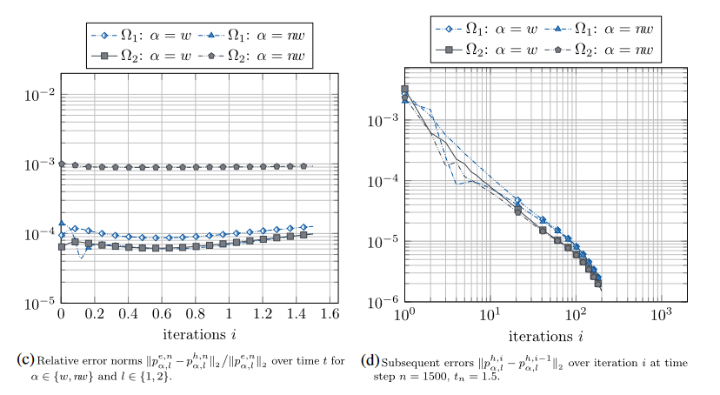
The viscous flow of two immiscible fluids in a porous medium on the Darcy scale is governed by a system of nonlinear parabolic equations. If infinite mobility of one phase can be assumed (e.g., in soil layers in contact with the atmosphere) the system can be substituted by the scalar Richards model. Thus, the porous medium domain maybe partitioned into disjoint subdomains where either the full two-phase or the simplified Richards model dynamics are valid. Extending the previously considered one-model situations we suggest coupling conditions for this hybrid model approach. Based on an Euler implicit discretization, a linear iterative (L-type) domain decomposition scheme is proposed, and proved to be convergent. The theoretical findings are verified by a comparative numerical study that in particular confirms the efficiency of the hybrid ansatz as compared to full two-phase model computations.

Adrian Florin Radu
Prof. Dr. rer. nat. habil.Research Project B03, Mercator Fellow

Christian Rohde
Prof. Dr. rer. nat.Deputy Spokesperson, Project Leader, Research Projects A05, B03, C02, Project MGK