SFB 1313 Publication "Coupling between a turbulent outer flow and an adjacent porous medium: High resolved Particle Image Velocimetry measurements"

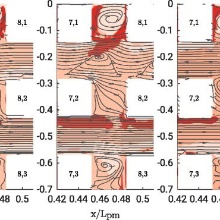
The existence of large-scale turbulent structures within a porous medium, generated through the interaction with a turbulent outer flow, is a highly debated topic, albeit most of the analysis is based on computational studies. This study contributes to the ongoing discussion by providing detailed point-measurements of the velocity in both regions by means of Particle Image Velocimetry (PIV). Two porous models of different porosity are investigated at three Reynolds numbers. The design of the experiments is based on theoretical studies to guarantee the presence of an unperturbed viscous layer at the interface (alias permeability Reynolds numbers of order one). Under these conditions and in compliance with theoretical predictions, the PIV data show the rapid dumping of turbulent fluctuations within the first pore cavities and can be used to validate closure models for volume-averaged computational studies. A point-data analysis is applied in the interfacial region by requiring continuity of tangential velocity and shear stress. The presence of the attached viscous layer implies that the coupling condition for momentum transfer must be controlled by shear, leading to the well-known Beavers and Joseph coupling condition. PIV data corroborate this statement and show the close interdependency between the penetration depth of the outer flow in the porous media and the characteristics of the vortical secondary flows induced by the strain rate at the pore scale. Consequently, the Beavers and Joseph-slip coefficient depends only upon the topology of the porous medium, at least as long as no transition to a perturbed mixing layer occurs at the interface.